1. AVL Tree

AVL Tree is based on BinarySearchTree. The most two common operations of a tree are ‘insert’ and ‘remove’ node. For these two operations, AVL Tree is almost the same to BinarySearchTree except the ‘balance’ process in the end of each ‘insert’ and ‘remove’.
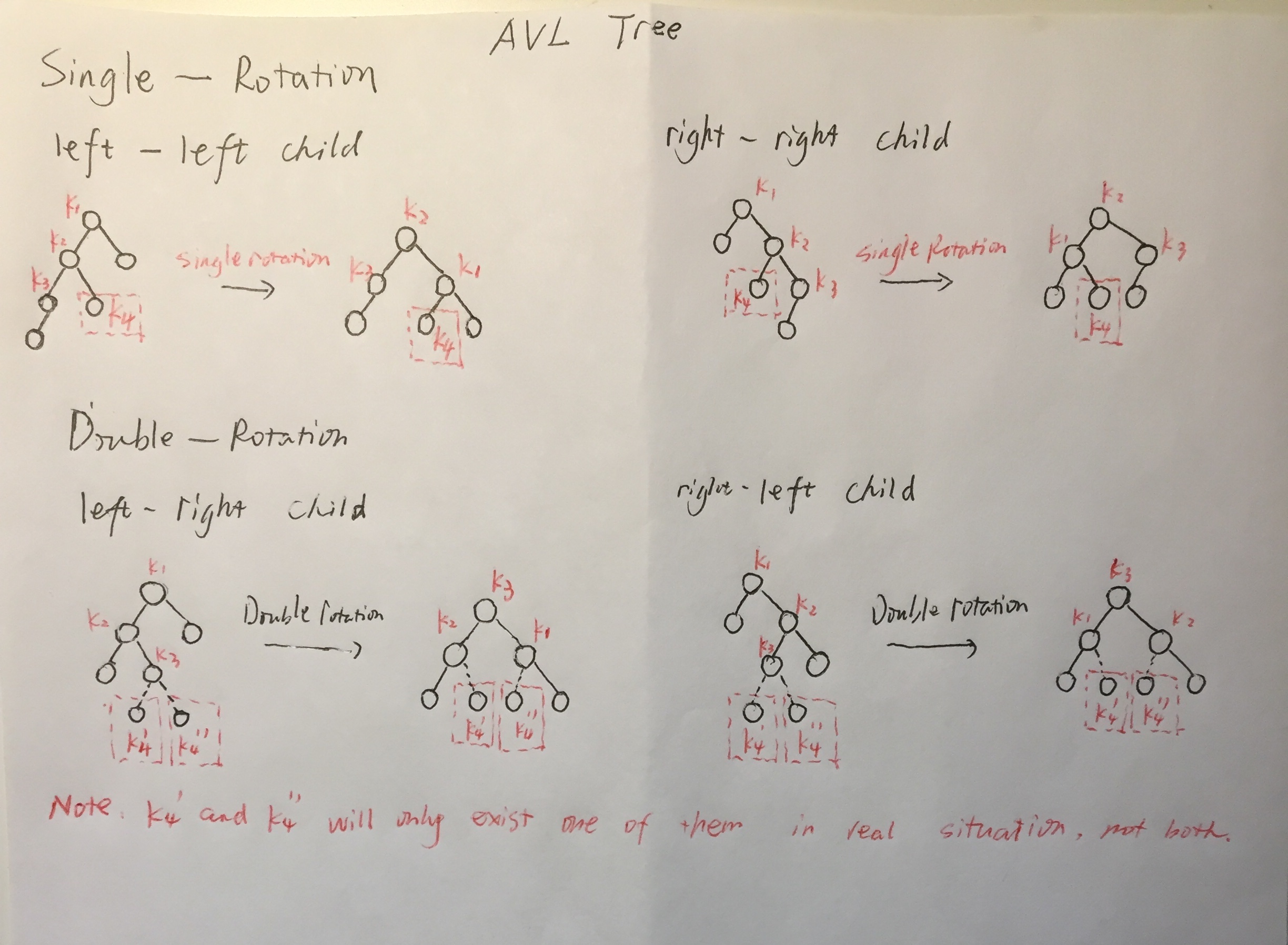
The ‘balance’ process is to check the height difference of every node’s left and right subtree, if the difference is greater than 1, that node needs to be rebalanced(rotated). And the rotation process includes two scenarios: single rotation and double rotation. Now, let’s dig deep into these two rotations.

Single Rotation

For single rotation, there are also two scenarios, which are ‘left child - left child’ and ‘right child- right child’.

• Left child - left child
  When writting codes for this condition, apart from the three major nodes(ancestor - left child - left child), do remember to switch the first left child’s right child to ancestor node’s new left child. For detailed explanation, please check the below graph.
• Right child - right child
  When writting codes for this condition, apart from the three major nodes(ancestor - right child - ritht child), do remember to switch the first right child’s left child to ancestor node’s new right child. For detailed explanation, please check the below graph.

Double Rotation

For double rotation, there are also two scenarios, which are ‘left child - right child’ and ‘right child - left child’.

• Left child - right child
  When writting code for this scenario, apart from the three major nodes(ancestor - left child - right child), do remember to switch the right child’s left or right child(it could be either child, but not both) to ancestor and left child’s new left or right child. For detailed explanation, please check the below graph.
• Right child - left child
  When writting code for this scenario, apart from the three major nodes(ancestor - right child - left child), do remember to switch the left child’s left or right child(it could be either child, but not both) to ancestor and right child’s new left or right child. For detailed explanation, please check the below graph.

After rotation process, we need to update the height of influenced nodes, where single rotation has two influenced nodes, while double rotation has three influenced nodes. For those nodes which don’t need to be rotated, we also need to set the height of the node.
Finally, we should return the new ‘root’ node after rotation.
Please check below graph for rotation details.